Oscilaciones
|
||
| Vamos a estudiar los modos normales de vibración de un sistema formado por muelles y partículas, como continuación y generalización del sistema formado por dos osciladores acoplados. Este ejemplo nos ayudará a comprender los modos normales de vibración de una cuerda fija por sus extremos, también denominados ondas estacionarias. Posteriormente, estudiaremos el mismo sistema formado por partículas y muelles, pero bajo la acción de una fuerza oscilante que actúa sobre la primera partícula. Buscaremos la fecuencia de los modos normales de oscilación a partir de la condición de resonancia, es decir, cuando la frecuencia de la fuerza oscilante coincide con alguna de las frecuencias propias del sistema.
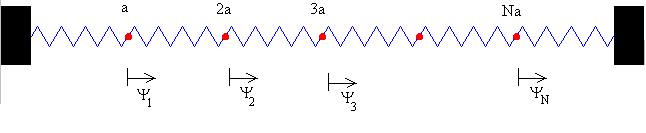
Modos normales de vibración de un sistema de muelles y partículasYa estudiamos las ecuaciones del movimiento de cada uno de los dos osciladores acoplados, por lo que será fácil, a partir de este ejemplo, generalizar el resultado para N osciladores. Como vemos en la figura, tenemos N partículas de masa m unidas a N+1 muelles iguales de constante K, cuyos extremos están fijos. La separación de equilibrio entre las partículas es a. Supongamos que en un instante dado t, la partícula 1 se desplaza y1, la partícula 2 se desplaza y2, ... la partícula i se desplaza yi, etc. La ecuación del movimiento para la partícula i será entonces
|
 |
Modos normalesSupongamos, que el sistema vibra en un modo de frecuencia w. Cada partícula describirá un M.A.S. de la misma frecuencia w y fase j , pero cuya amplitud Ai vamos a calcular. yi=Ai·cos(w t+j ) Introduciendo esta expresión en la ecuación diferencial que describe el movimiento de cada partícula, obtenemos, la relación entre las amplitudes de los M.A.S. de las partículas i+1, i, e i-1.
Vamos a buscar una solución a esta ecuación de la forma Ai=A·sen(k·ia) donde k es el número de onda k=2p /l . Después de algunas operaciones, se obtiene
y finalmente,
Esta ecuación que relaciona la frecuencia angular w con el número de onda k, se denomina relación de dispersión. Aplicaremos las condiciones de contorno para la solución buscada Ai=A·sen(kia) Las partículas imaginarias situadas en las posiciones extremas i=0, e i=N+1, están fijas, de aquí se obtiene los posibles valores del número de onda o de la longitud de onda. AN+1=A·sen(ka(N+1))=0, se cumple cuando ka(N+1)=np
La fórmula de las frecuencias angulares de los distintos modos de vibración son
Donde K es la constante del muelle, m la masa de las partículas, que hemos tomado como unidad, N el número de partículas del sistema. En la figura, se muestra la relación de dispersión para un sistema de 3 partículas. La curva continua en color azul es la representación de la frecuencia angular w en función del número de onda k, cuyo valor máximo se obtiene para k=p /a. Los puntos en color rojo sobre la curva continua señalan las frecuencias de los tres modos de vibración.
En el siguiente applet se van a mostrar de forma animada el movimiento de las partículas del sistema en el modo normal de vibración seleccionado. En la parte inferior del applet, se representa en el eje vertical el desplazamiento de cada una de las partículas. Como ejercicio se recomienda representar gráficamente, la frecuencia de los distintos modos en función del número de onda (o del número del modo n), tomando como modelo la figura anterior. Observar los modos de vibración de un sistema compuesto por muchas partículas y muelles, por ejemplo, 20, y compararlos con los modos de vibración de una cuerda u ondas estacionarias en una cuerda sujeta por ambos extremos. |
Instrucciones para el manejo del programaSe introduce
Se pulsa en el botón titulado Siguiente>> para observar el siguiente modo de vibración. Se pulsa en el botón titulado Anterior<< para observar el modo de vibración previo. En la parte superior de la ventana, se indica el modo normal de vibración n que se representa y su frecuencia w n.
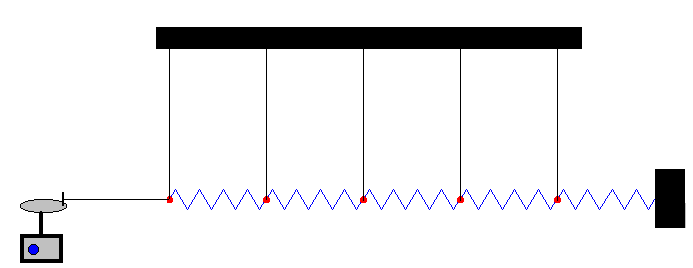
Oscilaciones forzadas de un sistema de partículas y muellesEn este apartado, vamos a simular una experiencia de laboratorio que consiste en un sistema de péndulos que unimos mediante muelles. El primero, lo unimos mediante una cuerda a una punta clavada en la periferia de un disco que gira accionado por un motor de velocidad variable, tal como se indica en la figura. |
 |
| La situación que se describe corresponde a las oscilaciones forzadas de un sistema formado por partículas y muelles. Se excita un determinado modo de vibración siempre que la frecuencia de la fuerza oscilante sea igual a la frecuencia de dicho modo de vibración, el sistema se dice entonces, que está en resonancia. En la sección anterior, hemos obtenido los distintos modos normales de vibración de un sistema, en ésta, observaremos cómo se excitan aplicando una fuerza oscilante de amplitud F0 y frecuencia angular wf, introduciendo en el control de edición titulado Frecuencia angular, el valor de la frecuencia del modo normal de vibración que se desea excitar. En el caso de que la amplitud de las oscilaciones sea grande, se disminuye la amplitud F0 de la fuerza oscilante, introduciendo un número más pequeño en el control de edición titulado Fuerza oscilante. Observar el comportamiento del sistema para otras frecuencias que no sean las de resonancia. En particular, frecuencias que estén por debajo de la frecuencia del primer modo, y frecuencias que estén por encima del modo de vibración más alto. |
Instrucciones para el manejo del programaSe introduce
Se ha de ajustar el valor de la amplitud para evitar que las partículas se desplacen demasiado disminuyéndola o aumentándola cuando se desplacen muy poco. |